1298: Monster-Hunter

“《怪物猎人：荒野》是一款非常好的游戏的说。”—— $LinXce$

$LinXce$ 最近沉迷于怪物猎人荒野，因为封印的龙骸布真的很酷。但是猎人工会的批准流程很麻烦，为了提升狩猎的速度，$LinXce$ 让阿尔玛一次批准狩猎多只怪物。

拿到了批准后，$LinXce$ 来到荒野。地图上记录了 $n$ 只怪物，第 $i$ 只怪物的坐标为 $(x_i, y_i)$，可能有多只怪物在同一个坐标。

但是怪物太多了，$LinXce$ 只能尽可能多狩猎一些。

作为他的随从艾露猫，你发明了呆猫玩偶，距离玩偶不超过 $r$ 的所有怪兽都会被吸引过来。（此处的距离为曼哈顿距离）

定义两点 $P$ 和 $Q$ 之间的距离为曼哈顿距离D，即： $$ D=|Px-Qx|+|Py-Qy| $$

呆猫玩偶很好用，但是只能使用一次。

现在你需要告诉 $LinXce$，在合适的位置使用呆猫玩偶之后，最多可以吸引来多少怪物？

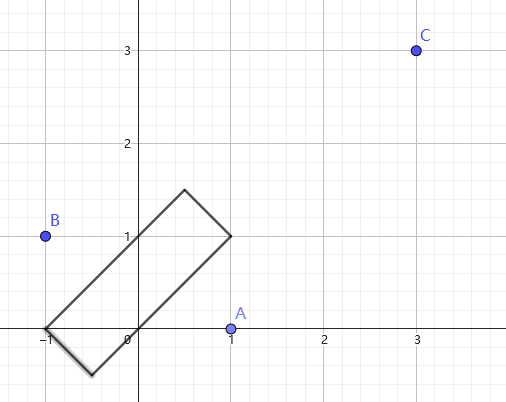
样例解释： 在框选区域内的所有点距离A，B点的曼哈顿距离都小于2。没有合适的位置使用呆猫玩偶能够吸引所有的怪物。

第 $1$ 行输入两个正整数 $n、r$ （$1 \leq n \leq 2*10^5$、$1 \leq r \leq 2*10^8$）

接下来 $n$ 行，每行输入两个整数 $x$、$y$，表示怪物的位置（$-10^8 \leq x、y \leq 10^8$）

输出一个整数 $d$ 表示最多能吸引多少怪物。

3 2
1 0
-1 1
3 3

2